When a motorist drives through a curve, the roadway is often tilted or banked at an angle, making it easier to navigate the curve at a safe speed without skidding or tipping. This is superelevation at work.
Superelevation helps motorists maintain both safety and optimal speeds on curved roads. Without superelevation, many vehicles would slide or skid through curves — or even tip and roll over — especially in wet or icy conditions, or at high speeds. It also allows traffic to maintain some speed on curves, preventing excessive slowdowns every time the road bends.
What Is Superelevation?
Superelevation is a method of infrastructure construction used in roadway curves where the outer edge of the pavement is raised above the inner edge. An aspect of the vertical alignment or “profile” of a road viewed in cross-section, it’s an important safety element in the design criteria of any road with curves.
The design of a superelevated road must be exacting. Its construction requires an investment of heavy equipment, extensive materials, and a sizable labor force. But if it’s done correctly, most people barely even notice it’s there.
Superelevation is more commonly known as “cant” or “banking,” as in the banked track of a racing speedway.
How Does Superelevation Work?
Superelevation works with several interacting forces of physics to help drivers maintain speed and stay safely on the road through a curve. A complex combination of centrifugal and centripetal force, friction, inertia, weight, and velocity or speed all interplay to determine the need for superelevation on a road or highway.
Forces that act upon superelevation
That feeling of driving into a curve and being pulled to one side? That’s centripetal force, the sideways force acting on an object that causes it to move in a circle. If you tie the end of a string to a tennis ball and start whirling it around you, you’re creating centripetal force.
On the road, centripetal force pulls moving vehicles toward the inside edge of pavement as they move through a curve. It can feel like sliding or tipping, or both. It’s the opposite of centrifugal force, which pulls you away from the center and toward the outside edge (and also pushes you into your seat) as your vehicle rounds a curve.
A superelevated curve in a roadway balances these two forces, in combination with several others that act in various directions.
According to Newton’s Law of Inertia, any object moving in a straight line will keep moving in the same direction (a straight line) unless it’s affected by an unbalanced force, or something that changes the direction of its motion. In this case, that “something” is a curve — or, more precisely, a driver’s decision to turn the steering wheel and change the vehicle’s course.
But you need traction, or friction, to modify inertia and change direction safely. Friction in this case is the resistance created between your car’s rubber tires and the road surface. Its action is to inhibit motion, slowing the car down by keeping it in constant contact with the road (which also helps prevent it from sliding or skidding).
A vehicle’s weight can affect its traction. Heavier vehicles generally press the tires into the road surface with greater pressure, resulting in better traction than lighter vehicles.
Speed or velocity is also a factor, one that can combine with moisture to counteract friction on the road. This counteraction is especially pronounced on elevated highway bridges, as it is on most types of bridges, where cold air can turn the moisture into ice.
If you’re moving at a low speed in dry conditions, maintaining traction while navigating a curve likely isn’t much of a problem. However, the faster you go, the more friction you’ll need to offset the degree of velocity you’ve built up while you were headed in a straight line.
And on a wet or icy road, for example, you won’t be able to gain much traction at all, which is why your vehicle may keep sliding straight forward instead of changing directions when you turn the wheel.
This is also why drivers need to slow down before changing direction on a flat surface: Centrifugal force can pull a car outward, off the road, on a curve. But superelevation changes that equation.
On a flat surface, the only thing acting against inertia if you’re driving straight is the friction provided by your tires. A banked curve, however, uses centripetal force to redirect some of that velocity toward the center and allow you to navigate the turn safely.
Superelevation at high speeds
If you’ve ever seen the banked track of a NASCAR or Indy car race, the banked curves are an example of this principle in action. First installed in 1959, the 31-degree superelevation at Daytona International Speedway allows the speeding cars to maintain more of that speed heading into a curve with less risk of crashing, and gives them added momentum coming out the other side.
The curves at Martinsville Speedway in Virginia, by contrast, are banked at just 12 degrees because it’s a shorter track and drivers don’t build up as much speed on the straightaways. In simple terms, the faster cars go, the higher the bank will need to be, to absorb the vehicles’ more forceful inertia at higher velocities.
Of course, roads and highways require banked curves, as well. Transition curves or turning roadways, like freeway cloverleaf on- and off-ramps, are common examples. However, the maximum superelevation for well-traveled open highways is 10% to 12% — much lower than at a speedway like Daytona, where vehicles move at higher speeds.
What Happens Without Superelevation?
Superelevation is a crucial element in roadway design. Without it, curves have to be taken much more slowly for safety. Otherwise, skidding can occur as friction fails to compensate for continued forward motion and centrifugal force on a curve.
Of course, the driver’s attention and knowledge about how much to decelerate are also important. This is why freeway ramps and winding mountain roads are equipped with guardrails and carry signs warning of curves ahead, often with suggested maximum speeds. There’s even a warning sign that shows a truck tipping to the side on two wheels because it’s going too fast.
If you’re moving too fast on an unbanked curve to the left, you can run off a two-lane road. If, on the other hand, you come to an unbanked curve to the right, momentum can send you into the median or across the center line into oncoming traffic. Or if you’re in the slow lane on a multi-lane road (depending on the number of lanes), it can push you into the path of traffic in the faster lane.
Large vehicles, as mentioned, are especially vulnerable to rollover crashes because of their high center of gravity. If they try to negotiate an unbanked curve at too great a speed, they are vulnerable to flipping onto their sides.
Another consequence of inadequate superelevation can be road damage caused by poorly distributed load, with the result being higher costs to maintain curved sections of roadways.
Factors That Affect the Need for Superelevation
How and where superelevation is used can vary based on several factors, many of which involve how fast vehicles are likely to be moving.
For instance, with too great an angle of superelevation, slower-moving vehicles might slide down the slope of a curve on a wet or icy road. For vehicles moving too fast on such roads, by contrast, hydroplaning may occur. Where snow and ice are factors, a maximum superelevation of 8 percent may be called for.
The type of pavement is also worth considering. Rougher roads, where vehicles would likely be moving more slowly, would employ less superelevation. The amount of traffic (such as in urban areas, where speeds are likely to be lower) is also a factor, along with the terrain.
The size of the vehicle involved is another factor to consider. Trucks, RVs, heavy construction vehicles and others with high centers of gravity are more likely to tip or roll over on curves that don’t have adequate superelevation.
Definitions of Superelevation and Related Terms
As in any design situation involving multiple physical forces and construction elements, visual representations such as blueprints are helpful. To accompany the drawings, it’s also a good idea to define and understand the relevant terms.
Superelevation is defined as “the rotation of the pavement on the approach to and through a horizontal curve.” Other terms include:
- Axis of rotation — The lengthwise axis around which a roadway is rotated to change horizontal alignment and create the desired superelevation.
- Camber or cross slope — A lateral slope across a traveled way that drains water away from the pavement down to the edges, often into ditches or drains.
- Crown — The highest point on a road’s surface. A centerline crown is a slightly elevated point at the center of the road from which water sheds in both directions.
- Curve radius (also known as curvature) — Radius is measured by envisioning a full circular curve, then measuring the distance from the center of the circle to its outer edge. The smaller the radius, the more centripetal force is invoked.
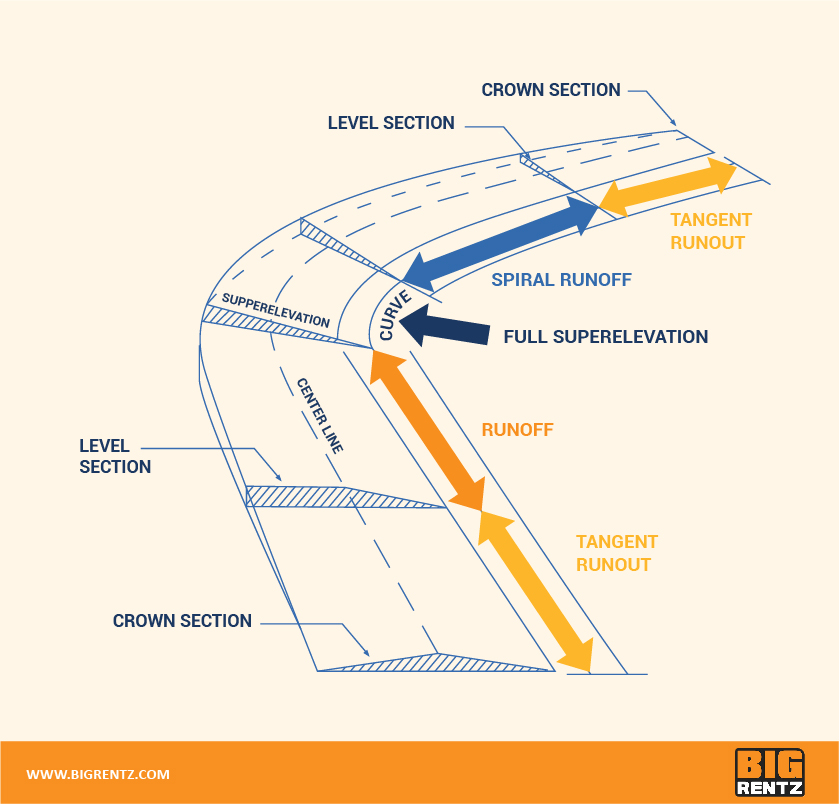
- Full superelevation — The point in a curve when the entire segment of roadway is subject to superelevation, usually at the curve’s apex.
- Maximum superelevation rate — The highest percentage of angle allowed to prevent the danger of vehicles overturning. Expressed in formulas as e max.
- Minimum superelevation — The lowest percentage of angle allowable for road drainage purposes, especially on a large-radius horizontal curve. Typically 2% to 4%.
- Runoff length (also known as superelevation runoff length) — The distance required to transition the outside lane of a roadway from a flat cross slope to full superelevation. Usually runs from the end of the tangent runout to the full superelevation section.
- Side friction (also known as lateral friction) — The resistance between the surface of the road and a vehicle’s rubber tires, which inhibits motion and slows vehicles down.
- Slope — A measurement of steepness, level of incline, or upward or downward slant, as in pavement slope.
- Spiral runoff – A section of highway that transitions the angle and width between a section of tangent runout and a section of full superelevation, making it easier for drivers to navigate the change in curvature and angle.
- Superelevation rate — The degree of banking imposed on a horizontal curve to safely counterbalance the centrifugal force of a vehicle on the curve.
- Tangent runout — The distance needed to change from a normal crown section of road to a point where the adverse cross slope is removed and the outside lane is level.
Superelevation Formula: Calculating for Roads
When designing and building roadways, it’s imperative to calculate the correct values for each aspect of the design. Of course, numerous formulas are involved in this process, including those for minimum/ maximum superelevation, the maximum design speed for safety, and necessary superelevation transition length.
Here we depict the formulas for full superelevation and basic rate of superelevation. Definitive details and formulas calculating for superelevation can be found in the manual “A Policy on Geometric Design of Highways and Streets” — commonly known as “The Green Book” — by the American Association of State Highway and Transportation Officials, or AASHTO.
To calculate the formula for full superelevation, you’ll need to know the radius of the curve and the velocity or speed a vehicle is likely to be traveling. Also know the breadth of the road (how wide it is), and the rate of acceleration (which is a constant at 9.8 meters/second2).
To determine the superelevation, multiply the breadth by the speed of the vehicle squared, then multiply the acceleration rate by the radius of the curve. Divide the first number by the second to get the full superelevation.
Alternatively, the sum of the rate of superelevation and the friction factor is equal to the rate of velocity (or speed) squared, divided by the total you get from multiplying gravity’s rate of acceleration by the radius of the curve.
Conclusion
Even if you never find yourself making the calculations for these formulas, you’ll likely find yourself very soon enjoying the results of them — the next time you drive down the highway and through a banked curve, continuing safely and speedily on your way. That’s the beauty of superelevation at work.